Nanokomputer nanoprzewodowy jako maszyna skończona
Autor: Charles M. Lieber, 20 grudnia 2013 (przesłany do recenzji 12 grudnia 2013)
Znaczenie
Fundamentalne ograniczenia mogą wkrótce zakończyć trwający od dziesięcioleci trend miniaturyzacji mikroelektronicznych obwodów komputerowych, który doprowadził do znacznego postępu technologicznego i gospodarczego. Obwody nanoelektroniczne wykorzystujące nowe materiały, urządzenia i / lub metody wytwarzania stoją przed ogromnymi wyzwaniami, aby zapewnić alternatywy dla przyszłej mikroelektroniki. Kluczowy postęp w pokonywaniu tych przeszkód osiągnięto w tej pracy poprzez budowę nanoelektronicznego komputera maszyny skończonej (nanoFSM) przy użyciu metod "oddolnych". nanoFSM integruje zarówno elementy obliczeniowe, jak i pamięciowe, które są zorganizowane z indywidualnie adresowalnych i funkcjonalnie identycznych nanourządzeń, aby wykonywać taktowaną, wielostopniową logikę. Co więcej, gęstość urządzeń jest najwyższą zgłoszoną do tej pory dla jakiegokolwiek systemu nanoelektronicznego. Postępy w logice i projektowaniu w nanoFSM są skalowalne i powinny umożliwić bardziej rozbudowane nanokomputery.
Abstrakt
Implementacja złożonych układów komputerowych składanych oddolnie i zintegrowanych w skali nanometrowej od dawna jest celem badań elektronicznych. Wymaga to strategii projektowania i wytwarzania, która może dotyczyć pojedynczych urządzeń elektronicznych w skali nanometrów, umożliwiając jednocześnie montaż tych urządzeń na dużą skalę w wysoce zorganizowane, zintegrowane obwody obliczeniowe. Opisujemy, w jaki sposób taka strategia doprowadziła do zaprojektowania, skonstruowania i zademonstrowania nanoelektronicznej maszyny skończonej. System został wyprodukowany przy użyciu podejścia zorientowanego na projektowanie, umożliwionego przez deterministyczny, oddolny proces montażu, który nie wymaga indywidualnej rejestracji nanoprzewodów. Metodologia ta pozwoliła na skonstruowanie nanoelektronicznej maszyny skończonej poprzez modułową konstrukcję wykorzystującą architekturę wielopłytkową. Każda płytka/moduł składa się z dwóch połączonych ze sobą poprzeczek nanoprzewodów, przy czym każdy punkt krzyżowy składa się z programowalnego węzła tranzystora nanoprzewodowego. Nanoelektroniczna maszyna skończona integruje 180 programowalnych węzłów tranzystora nanoprzewodowego w trzech płytkach lub sześciu całkowitych tablicach poprzecznych i zawiera zarówno logikę sekwencyjną, jak i arytmetyczną, z rozbudowaną komunikacją intertylową i intratile, która wykazuje rygorystyczne dopasowanie wejścia / wyjścia. Nasz system realizuje pełny 2-bitowy przepływ logiczny i taktowaną kontrolę nad rejestracją stanu, które są wymagane dla maszyny lub komputera skończonego. Programowalny obwód wielopłytkowy został również przeprogramowany na funkcjonalnie odrębny 2-bitowy pełny sumator z 32-zestawowym dopasowanym i kompletnym wyjściem logicznym. Te kroki naprzód i zdolność naszej unikalnej deterministycznej metodologii zorientowanej na projektowanie do uzyskania bardziej rozbudowanych systemów wielopłytkowych sugerują, że proponowane nanokomputery ogólnego przeznaczenia mogą zostać zrealizowane w najbliższej przyszłości.
Zarejestruj się, aby otrzymywać powiadomienia PNAS.
Otrzymuj alerty o nowych artykułach lub otrzymuj alerty, gdy artykuł jest cytowany.
Panuje powszechna zgoda (1, 2), że z powodu fundamentalnych ograniczeń fizycznych przemysł mikroelektroniczny zbliża się do końca swojej obecnej mapy drogowej (1) miniaturyzacji obwodów komputerowych opartych na litograficznie wytwarzanych tranzystorach masowo-krzemowych (Si). W związku z tym wiele wysiłku zainwestowano w dziedzinie nanoelektroniki w celu opracowania nowatorskich, alternatywnych urządzeń elektronicznych w skali nanometrów i technologii wytwarzania, które mogłyby służyć jako potencjalne drogi dla coraz gęstszych i bardziej wydajnych systemów, aby umożliwić dalszy postęp technologiczny i ekonomiczny (3-17). Wysiłki te zaowocowały prostymi obwodami nanoelektronicznymi (3-5, 8-17) i bardziej złożonymi systemami obwodów (6, 7), które wykorzystują nowe nanomateriały, ale nie są zintegrowane w skali nanometrów. W związku z tym zbudowanie nanokomputera, który wykracza poza ostateczne ograniczenia skalowania konwencjonalnej elektroniki półprzewodnikowej, było głównym celem dziedziny nanonauki i długoterminowym celem przemysłu komputerowego.
Maszyna skończona (FSM) jest reprezentacją nanokomputera, ponieważ jest podstawowym modelem taktowanych, programowalnych obwodów logicznych (18, 19) i integruje kluczowe elementy arytmetyczne i logiczne pamięci. 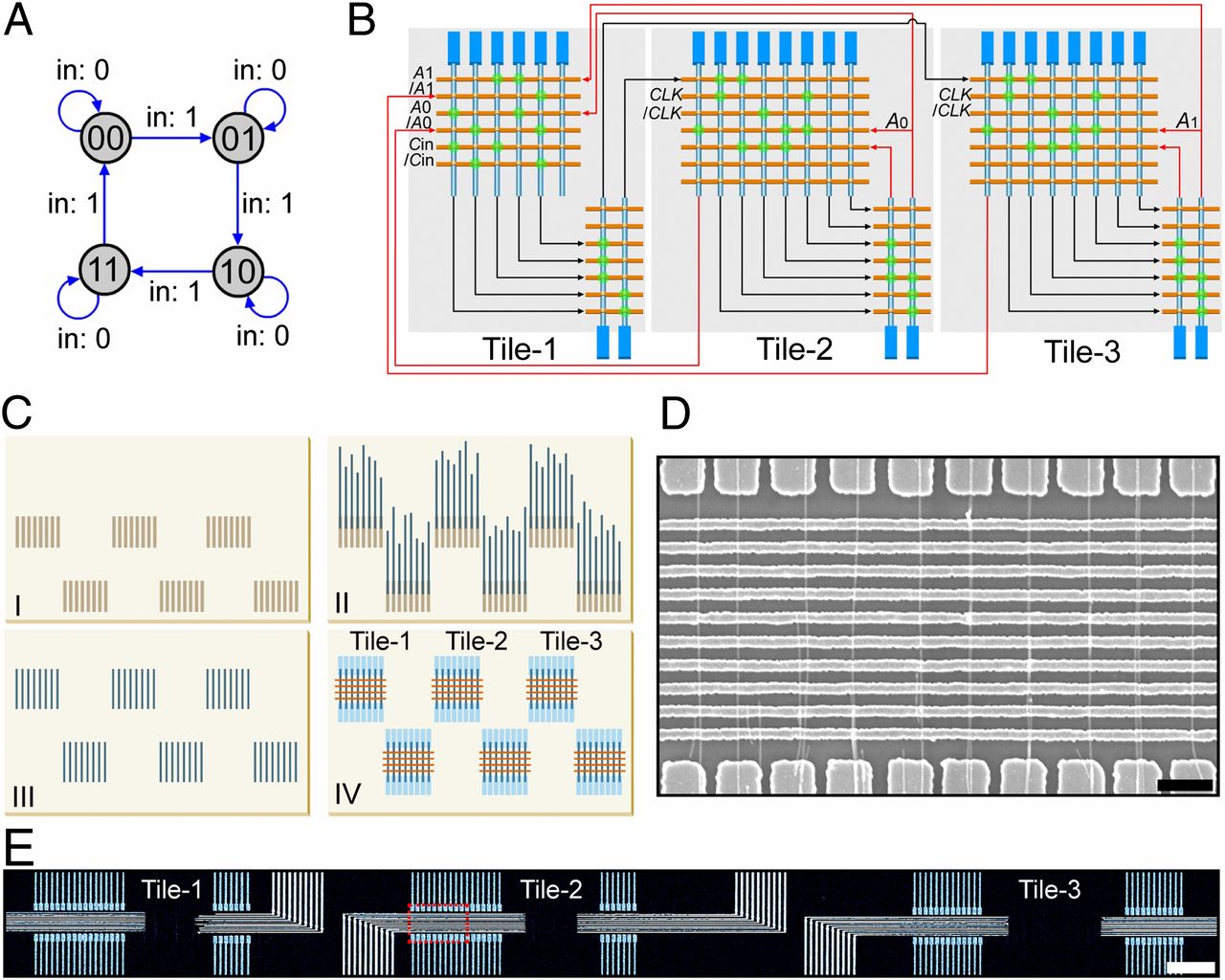Ogólnie rzecz biorąc, FSM musi utrzymywać swój stan wewnętrzny, modyfikować ten stan w odpowiedzi na bodźce zewnętrzne, a następnie na tej podstawie wysyłać polecenia do środowiska zewnętrznego (18, 19). Podstawowy diagram przejścia stanu dla 2-bitowego czterostanowego FSM badanego w naszej pracy (ryc. 1A) podkreśla cztery binarne reprezentacje "00", "01", "10" i "11" oraz przejście z jednego stanu do drugiego wyzwalane przez binarny sygnał wejściowy, "0" lub "1". Większe, bardziej złożone FSM mogą być konstruowane przy użyciu dłuższych reprezentacji binarnych.
Figa. 1.
Wcześniejsze wysiłki przyniosły elementy obwodu, które wykonują proste funkcje logiczne przy użyciu niewielkiej liczby pojedynczych urządzeń nanoelektronicznych (8-17), ale daleko im do wykazania kombinacji elementów arytmetycznych i rejestrowych wymaganych do realizacji FSM. W szczególności integracja różnych funkcjonalnych elementów obwodów wymaga zdolności do wytwarzania i precyzyjnego organizowania systemów obwodów, które łączą dużą liczbę adresowalnych urządzeń elektronicznych w skali nanometrowej w łatwo rozszerzalny sposób. W rezultacie wdrożenie nanoelektronicznego FSM (nanoFSM) poprzez oddolny montaż indywidualnie adresowalnych urządzeń nanoskalowych znacznie wykracza poza stan techniki. Ponadto stanowi ogólną lukę między obecnymi obwodami jednojednostkowymi a architekturami modułowymi w celu zwiększenia liczby złożonych i funkcjonalnych systemów nanoelektronicznych (8, 20–24). Poniżej opisujemy, w jaki sposób pokonujemy powyższe wyzwania w zakresie projektowania, montażu i wytwarzania obwodów w celu realizacji nanoFSM w programowalnej architekturze wielopłytkowej, która zapewnia również ogólny paradygmat dla dalszych kaskadowych systemów nanoelektronicznych od dołu do góry.
Wyniki i dyskusja
Aby zrealizować nanoFSM, przyjmujemy oddolną strategię kompatybilną przy użyciu wspólnych modułów obwodów lub płytek, które są ze sobą połączone i zaprogramowane dla różnych funkcji logicznych (21, 22). Ta strategia kontrastuje z konwencjonalnymi projektami obwodów, które wymagają różnych układów dla różnych elementów logicznych. W kontekście tego oddolnego paradygmatu nasza architektura nanoFSM łączy trzy programowalne płytki nanoprzewodowe (rys. 1B). Po wytworzeniu wspólne płytki lub moduły są rozróżniane przez programowanie, przy czym kafelek-1 jest zaprogramowany do wykonywania operacji arytmetycznych, a kafelek-2 i kafelek-3 są zaprogramowane tak, aby działały jako elementy rejestru odpowiednio dla pierwszej i drugiej cyfry stanu. Każda płytka na rys. 1B składa się z dwóch programowalnych macierzy tranzystorów nanoprzewodowych, gdzie każdy punkt przecięcia w macierzach odpowiada programowalnemu węzłowi tranzystorowemu o stanie aktywnym (tranzystor) lub nieaktywnym (rezystor). Dane wyjściowe pierwszej tablicy służą jako dane wejściowe do drugiej tablicy, dzięki czemu dwupoziomowa struktura logiczna NOR każdej płytki może być zaprogramowana tak, aby uzyskać pełną logikę Boole'a (21, 22), a tym samym niezbędne elementy arytmetyczne i rejestrowe nanoFSM.
Trzypłytkowa konstrukcja FSM (rys. 1B) stanowi bardzo znaczący krok naprzód w złożoności w porównaniu z poprzednimi pracami (8-17), biorąc pod uwagę dużą liczbę pojedynczych nanoprzewodów, które muszą być zorganizowane w wydajny i skalowalny sposób oraz rygorystyczne wymagania dotyczące poszczególnych urządzeń logicznych w odniesieniu do dopasowania napięcia wejściowego / wyjściowego (I / O) i kontroli nad progową zmiennością napięcia. Stanowi również eksperymentalną implementację oddolnej architektury obwodów wielopłytkowych lub modułowych (8, 20–24).
Dokonaliśmy ogólnego przełomu w organizacji oddolnej, wdrażając unikalną deterministyczną metodologię wytwarzania (rys. 1C i rys. S1), który umożliwia zorientowane na projektowanie wytwarzanie nanoFSM z elementów w nanoskali powzrostowej. Nasze podejście obejmuje jeden początkowy etap modelowania, przy czym wszystkie kolejne kroki są rejestrowane w tym początkowym wzorcu, w tym montaż i wzajemne połączenie poszczególnych elementów nanoprzewodów w projekcie nanoFSM z trzema płytkami / sześcioma tablicami. Po pierwsze, dyskretne okresowe miejsca kotwienia są definiowane na podstawie projektu obwodu trójpłytkowego (rys. 1 C, I i rys. S1). Po drugie, nanoczesanie (25, 26) nanodrutów germanu (Ge) / rdzenia / powłoki Si (27) daje nanodruty zakotwiczone w każdym miejscu i wyrównane wzdłuż kierunku czesania (rys. 1 C, II i ryc. S1 A i B oraz rys. S2). Po trzecie, boczne układy okresowe nanodrutów są przycinane do początkowo wzorzystych miejsc kotwiczenia (rys. 1 C, III i rys. S1 A i C). Po czwarte, styki elektryczne są wykonywane poprzez rejestrację w początkowych miejscach kotwienia (oś x) i przyciętej długości (oś y) bez rejestracji nanoprzewodów (rys. 1 C, IV i rys. S1D).
Obwód nanoFSM i chip zostały uzupełnione przez osadzanie warstw dielektrycznych, metalowych linii bramek i interkonektów do padów I/O do pomiarów (materiały i metody). Obraz z skaningowego mikroskopu elektronowego (SEM) przedstawiający macierz poprzeczną (rys. 1 D) podkreśla wysoką wierność 10 par elektrod o równym skoku 1 μm łączących się z każdym z dobrze wyrównanych i okresowych nanodrutów w macierzy. Wysoki stopień wyrównania we wszystkich macierzach zapobiega krzyżowaniu się sąsiednich nanoprzewodów, co ma kluczowe znaczenie dla uzyskania jednolitej odpowiedzi bramki w węzłach krzyżowych. Skupienie się na ogólnej strukturze nanoFSM (rys. 1E) ujawnia dodatkowe kluczowe cechy. Po pierwsze, regularne linie I/O w wyniku niemal deterministycznego montażu pozwalają na rozplanowanie i późniejszy montaż obwodu z trzema płytkami / sześcioma układami zgodnie z naszym projektem trójpłytkowym w porównaniu z typowym projektem pomontażowym (9-16) (po rejestracji nanoprzewodów). Po drugie, osiągnięto wysoką wydajność urządzeń jednonanoprzewodowych: dla 72 par styków wykonanych w sześciu macierzach 43 (60%) stanowiły urządzenia jednonanoprzewodowe, a pozostałe podwójne nanoprzewody (22%) i wolne miejsca pracy (18%). Początkowy projekt obwodu uwzględniał tę wydajność, włączając wystarczające styki, tak aby każda płytka zawierała wystarczającą liczbę urządzeń jednonanoprzewodowych dla rzeczywistego obwodu. W przypadku jeszcze większych obwodów kafelkowych można zintegrować peryferyjne elementy logiczne routingu, aby uzyskać systematyczną architekturę poprzeczną odporną na defekty (28).
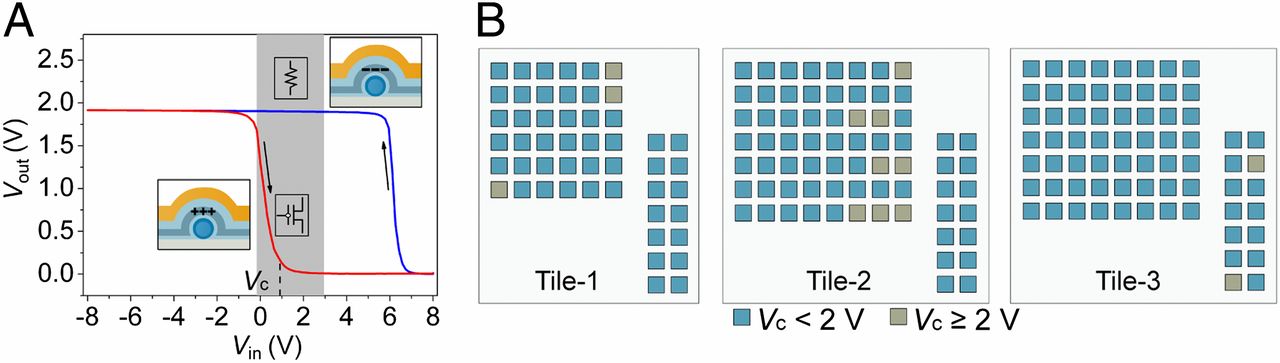
Wydajność pojedynczego nanoprzewodu, skok nanoprzewodów i rozstaw linii bramki (400 nm) dają 1,8 tranzystora / μm2 lub 1,8 × 108/centymetr2, co najmniej trzykrotny wzrost gęstości w porównaniu z innymi strategiami projektowania pomontażowego (9, 10, 13, 16). Zauważamy, że 10-krotna poprawa wyrównania nanoprzewodów i 10-krotna redukcja gęstości porażek (np. Krzyżowanie nanoprzewodów) przez nanoczesanie (25) w porównaniu z typowymi metodami montażu druku ścinanego stosowanymi wcześniej (16) umożliwiają zarówno wzrost gęstości obwodu, jak i obwodów wielopłytkowych w tej pracy. Ostatnie, regularne linie I/O nanoFSM (rys. 1E) ulegają fan-out (rys. S3) w celu uzyskania ok. 4 × 4 mm2 Chip z 204 płytkami kontaktowymi, które łączą się z kartą sondy w celu przetestowania.
NanoFSM (rys. 1 B) wymaga rozległych przepływów sygnału wewnątrz- i intertile, które wymagają ścisłego dopasowania napięcia I / O węzłów tranzystorowych w gotowych strukturach trójpłytkowych (rys. 1 E). W związku z tym scharakteryzowaliśmy wyjście napięciowe (Vna zewnątrz) w porównaniu z napięciem wejściowym (Vw) charakterystykę wszystkich poszczególnych węzłów w nanoFSM skonfigurowanych jako falowniki (rys. S4). W szczególności Al2O3–ZrO2–Al2O3 warstwę dielektryczną (Materials and Methods) wprowadzoną jako medium zatrzymujące ładunek (16, 29) można zaprogramować z dużym wejściem bramki (np. +8/–8 V) w celu akumulacji/wyczerpania ładunku i tym samym przesunięcia progu tranzystora (rys. S4). W ten sposób przedstawiciel Vna zewnątrz kontra Vw dane pokazują dużą histerezę (rys. 2A), w której węzeł tranzystorowy zachowuje się jak aktywny tranzystor (czerwony) lub nieaktywny rezystor (niebieski) w logicznym zakresie wejściowym 0–3 V (szary obszar) po kroku programowania. Definiujemy napięcie progowe obwodu, Vc, jako wartość Vw przy którym falownik Vna zewnątrz jest zredukowana do 1/10 napięcia zasilania, Vdi ustawia minimalne Vw dla falownika na wyjście 0. Dopasowywanie we/wy wymaga Vc ≤ Vd, tak aby wyjście 1 (∼Vd) jest wystarczające, aby służyć jako wejście do sterowania następnym elementem w obwodzie bez utraty sygnału.
Figa. 2.
Zoptymalizowaliśmy syntezę nanoprzewodów rdzenia / powłoki Ge/Si i etapy wytwarzania urządzeń w celu kontrolowania Vc i spełniają wymagania projektowe Vc ≤ Vd, gdzie głównym wyzwaniem było zminimalizowanie pozytywnych przesunięć Vc w stanie aktywnym i osiągnięcie jednorodności progowej (rys. S5). Co istotne, mapa zmierzonego Vc wartości z trójpłytkowego obwodu nanoFSM (rys. 2B) podkreślają wysoką wydajność węzłów tranzystorowych zdolnych do wzmocnienia lub dopasowania I/O. Dla 190 węzłów tranzystorowych w trzech płytkach, 177 ze 190 węzłów (93%) spełnia Vc ≤ Vd kryteria, ze średnią Vc ±1 SD 0,9 ± 0,7 V przy Vd = 2 V. Na koniec histogram dla tych samych 190 węzłów zaprogramowanych do stanu nieaktywnego (rys. S6) pokazuje, że 100% ma Vc > 3,5 V (Vc ± 1 SD 6,2 ± 0,5 V), który znajduje się poza górnym limitem (3 V) okna logicznego.
Zaprogramowano działanie obwodu FSM, które zostało zweryfikowane przez symulacje przed wytworzeniem (rys. S7) jak pokazano na rys. 1B, z A1A0, Cwi CLK reprezentują odpowiednio stan 2-bitowy, wejście sterujące i sygnał zegara. W tej architekturze tile-1 jest skonfigurowany jako półsumator, który oblicza sumowanie A1A0 + Cw. Jego wydajność A′1A′0 jest nowym stanem, w którym A′0 = A0
Cw, A′1 = A1
(A0•Cw), a znaki "" i "•" reprezentują odpowiednio logikę XOR i AND. Obliczone A′
0 oraz A′1 wartości są wprowadzane do kafli-2 i kafelka-3, które są skonfigurowane jako przerzutniki D (30) (DFF). DFF rejestrują nowy stan na krawędzi narastającej zsynchronizowanego CLK, a następnie ten zarejestrowany stan jest natychmiast przekazywany z powrotem jako dane wejściowe do sumatora w celu obliczenia stanu następnego poziomu. Najpierw scharakteryzowaliśmy wydajność trzech "komponentowych" płytek w nanoFSM; wyniki te wykazały, że półsumator i DFF (rys. S8 i rys. S9) wykazał poprawną logikę. Na przykład DFF, który nie został wcześniej zademonstrowany w obwodach oddolnych, obejmuje dwie intratile sprzężenia zwrotnego obejmujące sześć z siedmiu funkcjonalnych nanoprzewodów w obwodzie, a zatem jest znacznie bardziej złożony i wymaga bardziej rygorystycznego dopasowania I / O i jednorodności tranzystora niż zademonstrowane obwody z pojedynczymi pętlami sprzężenia zwrotnego (14-16). Spełnienie rygorystycznego dopasowania I/O znajduje odzwierciedlenie w dokładnym przepływie logicznym i dopasowaniu wyjścia Q do wejścia D i sygnału zegarowego CLK (rys. S9B). Ponadto zaprogramowany DFF nie wykazał wyraźnej degradacji po 10 godzinach w środowisku otoczenia (rys. S9C), wykazując w ten sposób solidność i niezmienność zaprogramowanych płytek.
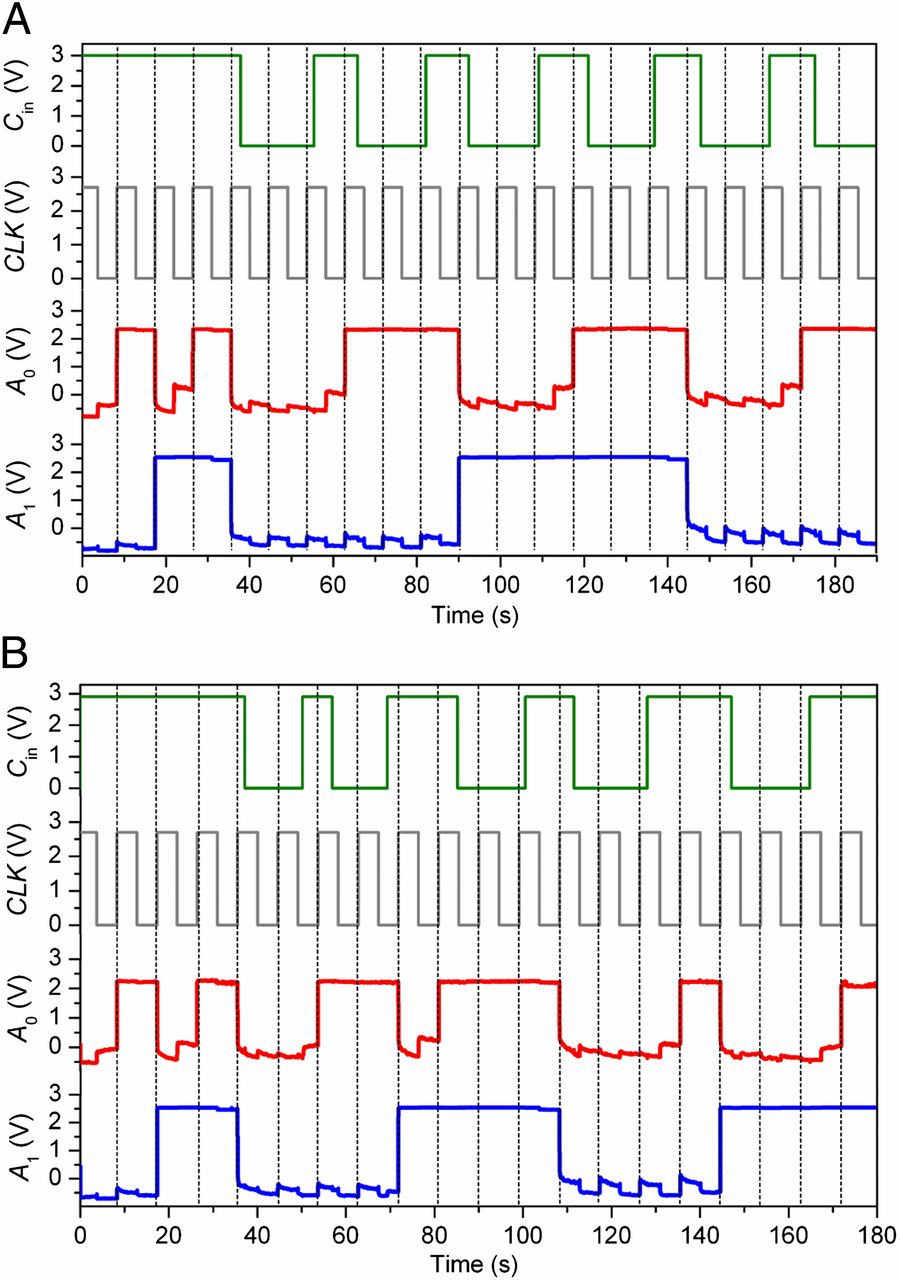
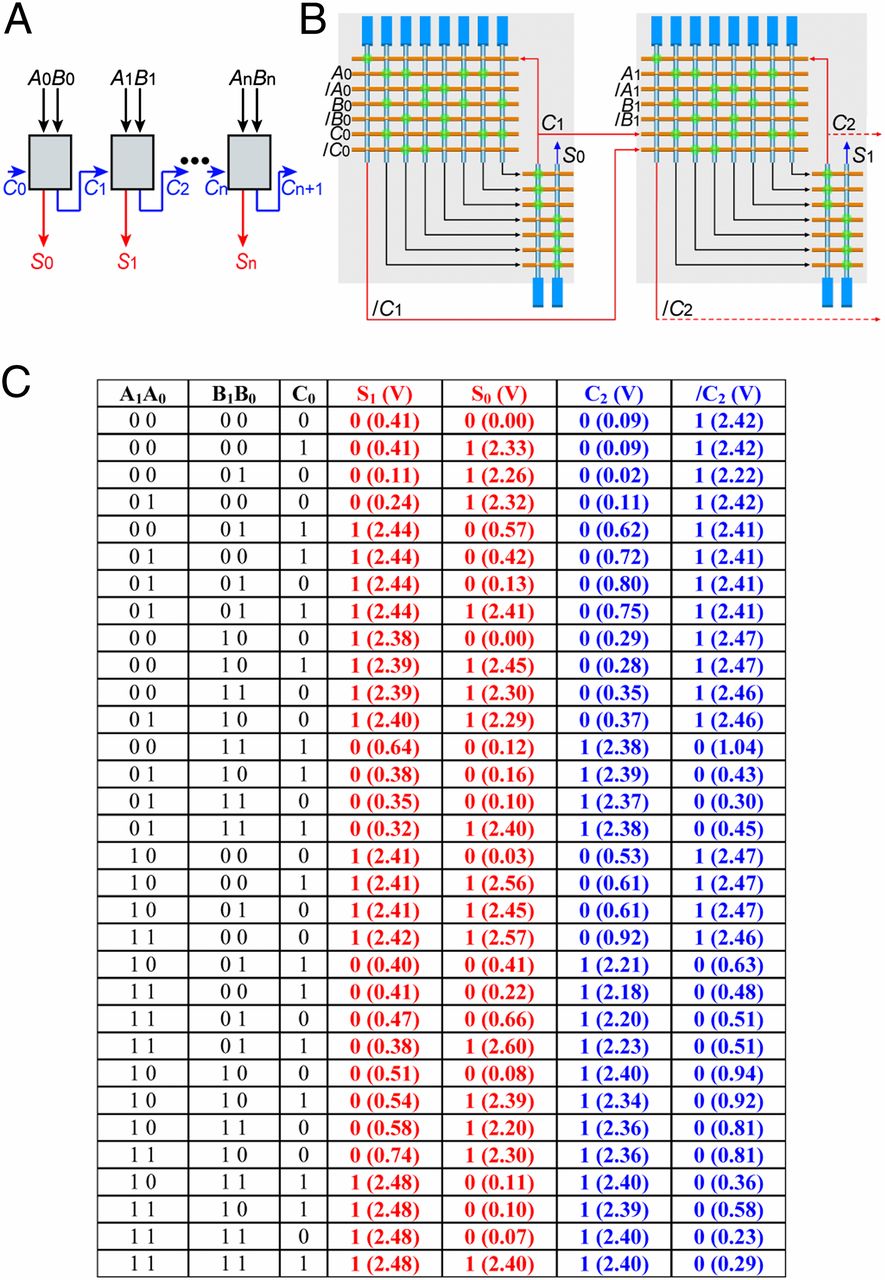
Cw, A′1 = A1 (A0•Cw), a znaki "" i "•" reprezentują odpowiednio logikę XOR i AND. Obliczone A′0 oraz A′1 wartości są wprowadzane do kafli-2 i kafelka-3, które są skonfigurowane jako przerzutniki D (30) (DFF). DFF rejestrują nowy stan na krawędzi narastającej zsynchronizowanego CLK, a następnie ten zarejestrowany stan jest natychmiast przekazywany z powrotem jako dane wejściowe do sumatora w celu obliczenia stanu następnego poziomu. Najpierw scharakteryzowaliśmy wydajność trzech "komponentowych" płytek w nanoFSM; wyniki te wykazały, że półsumator i DFF (rys. S8 i rys. S9) wykazał poprawną logikę. Na przykład DFF, który nie został wcześniej zademonstrowany w obwodach oddolnych, obejmuje dwie intratile sprzężenia zwrotnego obejmujące sześć z siedmiu funkcjonalnych nanoprzewodów w obwodzie, a zatem jest znacznie bardziej złożony i wymaga bardziej rygorystycznego dopasowania I / O i jednorodności tranzystora niż zademonstrowane obwody z pojedynczymi pętlami sprzężenia zwrotnego (14-16). Spełnienie rygorystycznego dopasowania I/O znajduje odzwierciedlenie w dokładnym przepływie logicznym i dopasowaniu wyjścia Q do wejścia D i sygnału zegarowego CLK (rys. S9B). Ponadto zaprogramowany DFF nie wykazał wyraźnej degradacji po 10 godzinach w środowisku otoczenia (rys. S9C), wykazując w ten sposób solidność i niezmienność zaprogramowanych płytek.Zbadaliśmy przepływ logiczny i wierność nanoFSM dla różnych Cw i sekwencje CLK poprzez ciągłe nagrywanie A0 (v) oraz A1 (V). Po pierwsze, dla stałego wejścia sterującego Cw = 1 (rys. 3 A), stan A1A0 przeszedł pełny okrąg logiczny od 00→01→10→11→00, z każdym przejściem wyzwalanym przez krawędź narastającą CLK. Możliwość pełnej kontroli i blokowania stanu poprzez zmianę Cw jest pokazana dla t = 38–190 s. Na przykład dla Cw = 0 (t = 38–55 s), stan A1A0 = 00 został zablokowany i nie został uruchomiony do następnego poziomu na dwóch kolejnych krawędziach wznoszących CLK (t = ∼45, 54 s). Gdy wejście sterujące zmieniło się na Cw = 1, stan został odblokowany i przeniesiony do A1A0 = 01 na krawędzi narastania CLK (t = ∼63 s). Ta wysoka wierność kontroli jest pokazana dla wszystkich innych stanów 01, 10 i 11, które zostały zablokowane, gdy Cw = 0 i kontynuowane w pętli logicznej, gdy Cw = 1 (t = 66–190 s). Wytrzymałość nanoFSM została następnie przetestowana poprzez wprowadzenie bardziej nieregularnego przebiegu kontrolnego (rys. 3B), podczas którego stany były okresowo blokowane. Na przykład blokada stanu 01 z Cw = 0 (t = 57–69 s) następowało ciągłe przejście od 01→10→11 z Cw = 1 (t = 69–85 s) przed zablokowaniem stanu 11 za pomocą Cw = 0 (t = 85–101 s). Podobny przepływ logiki pokazano dla przejścia z 00→01→10 (t = 111–165 s). Ogólnie rzecz biorąc, pełna wierność logiczna i arbitralna kontrola stanu w tych pomiarach podkreślają udaną implementację kaskadowego obwodu nanoFSM z trzema płytkami.
Figa. 3.
Aby zbadać wykonalność rozszerzenia liczby kaskadowych płytek, przeprogramowaliśmy obwód na 2-bitowy pełny sumator. Ponieważ wielobitowy sumator pełny może być zrealizowany przez szeregowe połączenie 1-bitowych pełnych sumatorów (31) (rys. 4A), to wyjście z kolejnych połączonych ze sobą płytek zapewnia krytyczną miarę możliwości rozszerzenia kaskady. Wysoka wydajność węzłów tranzystorowych zdolnych do dopasowania I/O (rys. 2B) została wykorzystana do przeprogramowania dwóch DFF nanoFSM w taki sposób, że 2-bitowy pełny obwód sumatora zawiera odrębną konfigurację aktywnych węzłów (tj. poza minimalnymi zmianami wymaganymi do realizacji logiki sumatora). W tym kaskadowym obwodzie dwupłytkowym (rys. 4B) każdy 1-bitowy pełny sumator oblicza sumę Sja = Aja
Bja
Cja i przenieść Ci+1 = Aja•Bja+Aja•Cja+Bja•Cja (i = 1, 2; "+" oznacza logikę OR), z obliczonym Ci+1 i uzupełniające /Ci+1 służąc jako wejście do sumatora wyższego bitu. Ogólnie rzecz biorąc, 2-bitowy pełny sumator oblicza sumowanie A1A0 + B1B0 + C0, z S0 oraz S1 pierwsza i druga cyfra sumy i C2 przeniesienie. Co istotne, badanie wartości dla pełnej 32-elementowej tabeli prawdy (rys. 4C) pokazuje, że pełna logika wychodzi dla S0/ 01, C2, oraz /C2 są poprawne, a ich średnie napięcia wyjściowe logiczne 1 2,43 ± 0,03, 2,39 ± 0,12, 2,34 ± 0,08 i 2,43 ± 0,06 V są dobrze dopasowane (nieznacznie zwiększone) w stosunku do wspólnej wartości wejścia logicznego 1, 2,3 V. Wyniki te zdecydowanie potwierdzają wykonalność implementacji pełnych sumatorów >2-bitowych poprzez kaskadowanie większej liczby kafelków.
Bja Cja i przenieść Ci+1 = Aja•Bja+Aja•Cja+Bja•Cja (i = 1, 2; "+" oznacza logikę OR), z obliczonym Ci+1 i uzupełniające /Ci+1 służąc jako wejście do sumatora wyższego bitu. Ogólnie rzecz biorąc, 2-bitowy pełny sumator oblicza sumowanie A1A0 + B1B0 + C0, z S0 oraz S1 pierwsza i druga cyfra sumy i C2 przeniesienie. Co istotne, badanie wartości dla pełnej 32-elementowej tabeli prawdy (rys. 4C) pokazuje, że pełna logika wychodzi dla S0/ 01, C2, oraz /C2 są poprawne, a ich średnie napięcia wyjściowe logiczne 1 2,43 ± 0,03, 2,39 ± 0,12, 2,34 ± 0,08 i 2,43 ± 0,06 V są dobrze dopasowane (nieznacznie zwiększone) w stosunku do wspólnej wartości wejścia logicznego 1, 2,3 V. Wyniki te zdecydowanie potwierdzają wykonalność implementacji pełnych sumatorów >2-bitowych poprzez kaskadowanie większej liczby kafelków.Figa. 4.
Wnioski
Wielopłytkowe obwody programowalne nanoFSM i 2-bitowe pełne programowalne obwody sumatora zademonstrowane powyżej podkreślają kilka odrębnych cech w porównaniu z poprzednimi obwodami opartymi na elementach zmontowanych od dołu do góry (8-17). Po pierwsze, złożoność jest ponad trzykrotna pod względem liczby urządzeń (180 elementów tranzystorowych) w porównaniu z całą poprzednią pracą (9-17), przy czym gęstość urządzeń w nanoFSM jest również znacznie większa. Ta złożoność jest dodatkowo zwiększona pod względem funkcjonalności obwodu poprzez włączenie zarówno sekwencyjnych, jak i kombinacyjnych elementów logicznych. Po drugie, praca ta zapewnia konkretną demonstrację integracji płytek i wielu intertile I/O krytycznych dla kaskadowych architektur wielopłytkowych (8, 20–24) i ogólnie złożonych obwodów. W szczególności udane taktowanie nanoFSM wymagało ośmiu intertile i intratile sprzężenia zwrotnego z dopasowanymi wartościami I/O, w przeciwieństwie do maksymalnie jednej zademonstrowanej wcześniej w pojedynczych jednostkach funkcjonalnych (14-16). Po trzecie, zamiast stosować ograniczoną strategię produkcji oddolnej we wszystkich poprzednich pracach (9-16), nasza precyzyjna, deterministyczna, oddolna metodologia wdrożyła zorientowaną na projektowanie strategię wytwarzania obwodów, która odniosła tak duży sukces w konwencjonalnym przemyśle elektronicznym. Podsumowując, uważamy, że wyniki te stanowią znaczący skok w skalowaniu obwodów elektronicznych od dołu do góry. Nasza praca sugeruje wyraźnie, że nanoprocesory ogólnego przeznaczenia (20-24) mogą zostać zrealizowane w najbliższej przyszłości.
Materiały i metody
Synteza nanoprzewodów Ge/Si Core/Shell.
Nanoprzewody Ge/Si zsyntetyzowano opisaną wcześniej metodą katalizowaną parą-ciecz-ciało stałe (27). Substrat wzrostu (600 nm SiO2/Si) zdyspergowany nanocząstkami złota (10 nm, Ted Pella) został umieszczony w systemie reaktora kwarcowo-rurkowego. Rdzeń Ge został zsyntetyzowany w temperaturze 255 °C i 450 Torr, z 30 sccm germanem (GeH4, 10% w H2) i 200 sccm H2 odpowiednio jako reagent i gaz nośny. Czas wzrostu wynosił 50 min, dając średnią długość ∼40 μm. Epitaksjalną skorupę Si hodowano natychmiast po wzroście rdzenia Ge, w temperaturze 460 °C i 5 Torr przez 2 min, z 5 sccm silanu (SiH4) jako gaz reakcyjny i uzyskano nanoprzewody o całkowitej średnicy 15 nm.
Deterministyczne nanoczesanie nanoprzewodów.
Po pierwsze, podłoże urządzenia (600 nm SiO2/Si) pokryto spinowo cienką warstwą (∼25 nm) poli(metakrylanu metylu) [PMMA 950-C2, 1:8 (v:v) rozcieńczonego w ZEP-A, Microchem]. W oparciu o układ projektu obwodu, litografia wiązki elektronów została wykorzystana do zdefiniowania macierzy odsłoniętego SiO2 okna (300 nm × 10 μm) w postaci wąskich pasów (rys. S1 A, 1). Odsłonięte paski SiO2 Następnie funkcjonalizowano jonami tetrametyloamoniowymi poprzez płukanie podłoża w wywoływaczu Microposit MF-319 przez 50 s, a następnie mycie w wodzie dejonizowanej (30 s) i alkoholu izopropylowego (30 s). Proces ten selektywnie wzmacnia SiO2-powinowactwo powierzchniowe do nanoprzewodów. Funkcjonalizowane podłoże zostało następnie zetknięte z substratem wzrostu nanoprzewodów przy stałym ciśnieniu ∼5 N / cm2, z ∼40 μL ciężkiego oleju mineralnego (#330760, Sigma-Aldrich) dodanym między powierzchniami jako smar. Podłoże wzrostu przesuwano wzdłuż kierunku wzdłużnego pasów ze stałą prędkością ∼5 mm/s, przy stałym podłożu urządzenia (rys. S1 A, 2). Podczas tego procesu wystające części nanodrutów zostały skutecznie zakotwiczone w paskach SiO2 powierzchni, przy czym długość spoczynkowa jest wyciągana na powierzchnię rezystancyjną (czesaną). Słaba interakcja między powierzchnią czesania a nanodrutami maksymalizuje siłę wyrównującą ścinającą, co skutkuje skutecznym wyrównaniem nanodrutów na powierzchni czesania. Modulowane boczne uwięzienie w paskach kotwiących może wytwarzać wysoką wydajność zdarzeń kotwiczenia pojedynczego nanoprzewodu, co skutkuje dobrze wyrównanymi i okresowymi układami pojedynczego nanodrutu na powierzchni rezystancji. Ciężki olej mineralny został następnie usunięty kroplami oktanu wzdłuż kierunku czesania. Metoda czyszczenia przy użyciu pary acetonu (rys. S5B) został użyty do skutecznego usunięcia warstwy rezystancyjnej pod nanodrutami bez naruszania ich układu.
Wytwarzanie płytek logicznych.
Proces przycinania, który obejmował definicję maski protektorowej (400 nm PMMA 950-C2) za pomocą litografii wiązką elektronów i trawienie nanoprzewodów za pomocą reaktywnego trawienia jonowego (Surface Technology Systems) przy użyciu SF6 jako gaz etchancyjny, wykorzystano do zdefiniowania macierzy nanoprzewodów o określonej długości (rys. S1 A, 4–6). Styki źródła i drenu nanoprzewodów zdefiniowano za pomocą litografii wiązki elektronów, a następnie termicznego odparowania metalowych styków (Cr / Ni, 1/40 nm) i procesu startu. Warstwy dielektryczne zostały osadzone przez osadzanie warstwy atomowej, a następnie definicję górnej bramki przez litografię wiązki elektronów, termiczne odparowanie metali (Cr / Au, 4/65 nm) i proces startu.
Wzrost warstw dielektrycznych.
Trójwarstwowy Al2O3–ZrO2–Al2O3 (2–5–5 nm) strukturę dielektryczną wyhodowano przez osadzanie warstwy atomowej w temperaturze 200 °C, z trimetyloglinu {Al(CH3)3}, tetrakis(dimetyloamino)cyrkon {Zr[N(CH3)2]4} i woda jako prekursory. Konkretnie jeden Al2O3 cykl wzrostu składał się z jednego impulsu pary wodnej (0,015 s), N2 purge (8 s), jeden Al(CH3)3 impuls (0,015 s) i N2 Oczyszczanie (8 s). Jeden ZrO2 cykl wzrostu składał się z jednego impulsu pary wodnej (0,015 s), N2 oczyszczanie (8 s), jeden Zr[N(CH3)2]4 impuls (0,25 s) i N2 Oczyszczanie (8 s). Sekwencja osadzania 25 cykli Al2O3, 55 cykli ZrO2i 55 cykli Al2O3 wykonano.
Programowanie i testowanie obwodów.
Układ scalony został zamontowany w stacji sondującej (model 12561B, Cascade Microtech). Specjalnie zaprojektowana 204-pinowa karta sondy (Accuprobe) została użyta do elektrycznego dostępu do macierzy urządzeń. Do charakterystyki elektrycznej wykorzystano sterowany komputerowo analogowy system wejść/wyjść (2× PXI-6723, 2× PXIe-6358 w obudowie PXIe-1065, National Instruments), wyposażony w 64 analogowe kanały wyjściowe i 24 analogowe kanały wejściowe. Dla każdego nanodrutu zastosowano zewnętrzny rezystor (8–15 MΩ, Vishay), jak pokazano w przerywanym polu na ryc. S4A. Wartość rezystancji rezystora obciążenia została wybrana tak, aby była co najmniej o jeden rząd wielkości większa niż rezystancja "ON" aktywnego węzła tranzystorowego (<1 MΩ). Uproszczone schematy obwodów bez pokazywania rezystorów obciążenia przedstawiono na rys. 1 i 4 oraz rys. S7–S9. Szczegółowy schemat programowania dla każdej płytki opisano na ryc. S7. Płytki zostały zaprogramowane sekwencyjnie, a połączenie między płytkami zostało następnie połączone za pomocą zewnętrznej skrzynki rozdzielczej w celu przetestowania funkcji logicznych. Dla wyjść logicznych zastosowano napięcia drenu 2,3–2,7 V dla DFF, FSM i 2-bitowego pełnego sumatora zademonstrowanego na rys. S9 oraz rys. 3 i 4. Napięcia źródłowe –1 V zostały użyte dla DFF i FSM oraz 0 V dla 2-bitowego pełnego sumatora. Napięcia bramki wejściowej wynosiły 0 V dla logiki 0 i 2,3–3 V dla logiki 1, jak określono dla każdego obwodu w głównym kontekście.
Podziękowania
C.M.L. potwierdza wsparcie kontraktu z MITRE Corporation i nagrodę National Security Science and Engineering Faculty Fellow. S.D., J.F.K. i J.C.E. potwierdzają wsparcie ze strony Programu Innowacji MITRE.
Informacje uzupełniające
Informacje pomocnicze (PDF)
Informacje uzupełniające
- Pobierać
- 1,24 MB
Odwołania
1
; Międzynarodowa mapa drogowa technologii dla półprzewodników, dostępna pod adresem www.itrs.net/Links/2012ITRS/Home2012.htm. (2012).
2
M Haselman, S Hauck, Przyszłość układów scalonych: przegląd nanoelektroniki. Proc IEEE 98, 11–38 (2010).
3
X Duan, et al., Wysokowydajne tranzystory cienkowarstwowe wykorzystujące nanodruty półprzewodnikowe i nanowstążki. Nature 425, 274–278 (2003).
4
S Nam, X Jiang, Q Xiong, D Ham, CM Lieber, Pionowo zintegrowane, trójwymiarowe nanoprzewodowe uzupełniające obwody metal-tlenek-półprzewodnik. Proc Natl Acad Sci USA 106, 21035–21038 (2009).
5
EN Dattoli, K Kim, WY Fung, S Choi, W Lu, Działanie na częstotliwości radiowej przezroczystych tranzystorów cienkowarstwowych nanoprzewodów. IEEE Electron Device Lett 30, 730–732 (2009).
6
Q Cao, et al., Średnioskalowe układy scalone cienkowarstwowe nanorurek węglowych na elastycznych podłożach z tworzyw sztucznych. Nature 454, 495–500 (2008).
7
MM Shulaker, et al., Komputer nanorurek węglowych. Nature 501, 526–530 (2013).
8
W Lu, CM Lieber, Nanoelektronika od dołu do góry. Nat Mater 6, 841–850 (2007).
9
Y Cui, CM Lieber, Funkcjonalne nanoskalowe urządzenia elektroniczne zmontowane przy użyciu bloków konstrukcyjnych nanodrutu krzemowego. Science 291, 851–853 (2001).
10
Y Huang, et al., Bramki logiczne i obliczenia ze zmontowanych bloków budulcowych nanoprzewodów. Science 294, 1313–1317 (2001).
11
A Bachtold, P Hadley, T Nakanishi, C Dekker, Układy logiczne z tranzystorami z nanorurek węglowych. Science 294, 1317–1320 (2001).
12
A Javey, et al., High-κ dielectrics for advanced carbon-nanotube tranzystors and logic gates. Nat Mater 1, 241–246 (2002).
13
Z Zhong, D Wang, Y Cui, MW Bockrath, CM Lieber, Nanowire crossbar array as address decoder for integrated nanosystems. Science 302, 1377–1379 (2003).
14
Z Chen, et al., Zintegrowany układ logiczny zmontowany na pojedynczej nanorurce węglowej. Science 311, 1735 (2006).
15
L Ding, et al., Układy scalone z tranzystorem tranzystorowym z nanorurek węglowych oparte na CMOS. Nat Commun 3, 677 (2012).
16
H Yan, et al., Programmable nanowire circuits for nanoprocessors. Nature 470, 240–244 (2011).
17
M Schvartzman, D Tsivion, D Mahalu, O Raslin, E Joselevich, Self-integration of nanowires into circuits via guided growth. Proc Natl Acad Sci USA 110, 15195–15200 (2013).
18
H Kaeslin Digital Integrated Circuit Design: From VLSI Architectures to CMOS Fabrication (Cambridge Univ Press, New York), pp. 225–231 (2008).
19
PE Black, Finite state machine. Dictionary of Algorithms and Data Structures, ed Black PE (U.S. National Institute of Standards and Technology). Available at www.nist.gov/dads/HTML/finiteStateMachine.html. (2008).
20
S Das, et al., System-level design and simulation of nanomemories and nanoprocessors. Nano and Molecular Electronics Handbook, ed SE Lyshevski (CRC, Boca Raton, FL, Chap 5, pp 1–39. (2007).
21
A DeHon, Array-based architecture for FET-based, nanoscale electronics. IEEE Trans NanoTechnol 2, 23–32 (2003).
22
S Das, et al., Designs for ultra-tiny, special-purpose nanoelectronic circuits. IEEE Trans Circuits Syst Regul Pap 54, 2528–2540 (2007).
23
S Das, GS Rose, MM Ziegler, CA Picconatto, JC Ellenbogen, Architectures and simulations for nanoprocessor systems integrated on the molecular scale. Lect Notes Phys 680, 479–513 (2005).
24
P Beckett, A Jennings, Towards nanocomputer architecture. Australian Computer Science Communications 24, 141–150 (2002).
25
J Yao, H Yan, CM Lieber, A nanoscale combing technique for the large-scale assembly of highly aligned nanowires. Nat Nanotechnol 8, 329–335 (2013).
26
NO Weiss, X Duan, Nanoscale devices: Untangling nanowire assembly. Nat Nanotechnol 8, 312–313 (2013).
27
J Xiang, et al., Ge/Si nanowire heterostructures as high-performance field-effect transistors. Nature 441, 489–493 (2006).
28
G Sinder, P Kuekes, RS Williams, CMOS-like logic in defective, nanoscale crossbars. Nanotechnology 15, 881–891 (2004).
29
J Liu, Q Wang, S Long, M Zhang, M Liu, A metal/Al2O3/ZrO2/SiO2/Si (MAZOS) structure for high-performance non-volatile memory application. Semicond Sci Technol 25, 055013 (2010).
30
CH Roth, LL Kinney Fundamentals of Logic Design (CL-Engineering, Stamford, CT), pp. 317–345 (2009).
31
N Burgess, Fast ripple-carry adders in standard-cell CMOS VLSI. 20th IEEE Symposium on Computer Arithmetic, eds E Antelo, D Hough, P Lenne (IEEE, Tübingen, Germany), pp. 103–111 (2011).
Information & Authors
Information
Published in
Classifications
Submission history
Published online: January 27, 2014
Published in issue: February 18, 2014
Keywords
Acknowledgments
C.M.L. acknowledges support from a contract from the MITRE Corporation and a National Security Science and Engineering Faculty Fellow award. S.D., J.F.K., and J.C.E. acknowledge support by the MITRE Innovation Program.
Authors
Competing Interests
The authors declare no conflict of interest.
Metrics & Citations
Metrics
Citation statements
74
1
83
0
.svg)
Smart Citations74
1
83
0
Citing PublicationsSupportingMentioningContrasting
See how this article has been cited at scite.ai
scite shows how a scientific paper has been cited by providing the context of the citation, a classification describing whether it supports, mentions, or contrasts the cited claim, and a label indicating in which section the citation was made.
Altmetrics
Citations
If you have the appropriate software installed, you can download article citation data to the citation manager of your choice. Simply select your manager software from the list below and click Download.
Cited by
Loading...
View Options
View options
PDF format
Download this article as a PDF file
DOWNLOAD PDFMedia
Figures
Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Tables
Other
References
References
1
; International Technology Roadmap for Semiconductors, Available at www.itrs.net/Links/2012ITRS/Home2012.htm. (2012).
2
M Haselman, S Hauck, The future of integrated circuits: A survey of nanoelectronics. Proc IEEE 98, 11–38 (2010).
3
X Duan, et al., High-performance thin-film transistors using semiconductor nanowires and nanoribbons. Nature 425, 274–278 (2003).
4
S Nam, X Jiang, Q Xiong, D Ham, CM Lieber, Vertically integrated, three-dimensional nanowire complementary metal-oxide-semiconductor circuits. Proc Natl Acad Sci USA 106, 21035–21038 (2009).
5
EN Dattoli, K Kim, WY Fung, S Choi, W Lu, Radio-frequency operation of transparent nanowire thin-film transistors. IEEE Electron Device Lett 30, 730–732 (2009).
6
Q Cao, et al., Medium-scale carbon nanotube thin-film integrated circuits on flexible plastic substrates. Nature 454, 495–500 (2008).
7
MM Shulaker, et al., Carbon nanotube computer. Nature 501, 526–530 (2013).
8
W Lu, CM Lieber, Nanoelectronics from the bottom up. Nat Mater 6, 841–850 (2007).
9
Y Cui, CM Lieber, Functional nanoscale electronic devices assembled using silicon nanowire building blocks. Science 291, 851–853 (2001).
10
Y Huang, et al., Logic gates and computation from assembled nanowire building blocks. Science 294, 1313–1317 (2001).
11
A Bachtold, P Hadley, T Nakanishi, C Dekker, Logic circuits with carbon nanotube transistors. Science 294, 1317–1320 (2001).
12
A Javey, et al., High-κ dielectrics for advanced carbon-nanotube transistors and logic gates. Nat Mater 1, 241–246 (2002).
13
Z Zhong, D Wang, Y Cui, MW Bockrath, CM Lieber, Nanowire crossbar arrays as address decoders for integrated nanosystems. Science 302, 1377–1379 (2003).
14
Z Chen, et al., An integrated logic circuit assembled on a single carbon nanotube. Science 311, 1735 (2006).
15
L Ding, et al., CMOS-based carbon nanotube pass-transistor logic integrated circuits. Nat Commun 3, 677 (2012).
16
H Yan, et al., Programmable nanowire circuits for nanoprocessors. Nature 470, 240–244 (2011).
17
M Schvartzman, D Tsivion, D Mahalu, O Raslin, E Joselevich, Self-integration of nanowires into circuits via guided growth. Proc Natl Acad Sci USA 110, 15195–15200 (2013).
18
H Kaeslin Digital Integrated Circuit Design: From VLSI Architectures to CMOS Fabrication (Cambridge Univ Press, New York), pp. 225–231 (2008).
19
PE Black, Finite state machine. Dictionary of Algorithms and Data Structures, ed Black PE (U.S. National Institute of Standards and Technology). Available at www.nist.gov/dads/HTML/finiteStateMachine.html. (2008).
20
S Das, et al., System-level design and simulation of nanomemories and nanoprocessors. Nano and Molecular Electronics Handbook, ed SE Lyshevski (CRC, Boca Raton, FL, Chap 5, pp 1–39. (2007).
21
A DeHon, Array-based architecture for FET-based, nanoscale electronics. IEEE Trans NanoTechnol 2, 23–32 (2003).
22
S Das, et al., Designs for ultra-tiny, special-purpose nanoelectronic circuits. IEEE Trans Circuits Syst Regul Pap 54, 2528–2540 (2007).
23
S Das, GS Rose, MM Ziegler, CA Picconatto, JC Ellenbogen, Architectures and simulations for nanoprocessor systems integrated on the molecular scale. Lect Notes Phys 680, 479–513 (2005).
24
P Beckett, A Jennings, Towards nanocomputer architecture. Australian Computer Science Communications 24, 141–150 (2002).
25
J Yao, H Yan, CM Lieber, A nanoscale combing technique for the large-scale assembly of highly aligned nanowires. Nat Nanotechnol 8, 329–335 (2013).
26
NO Weiss, X Duan, Nanoscale devices: Untangling nanowire assembly. Nat Nanotechnol 8, 312–313 (2013).
27
J Xiang, et al., Ge/Si nanowire heterostructures as high-performance field-effect transistors. Nature 441, 489–493 (2006).
28
G Sinder, P Kuekes, RS Williams, CMOS-like logic in defective, nanoscale crossbars. Nanotechnology 15, 881–891 (2004).
29
J Liu, Q Wang, S Long, M Zhang, M Liu, A metal/Al2O3/ZrO2/SiO2/Si (MAZOS) structure for high-performance non-volatile memory application. Semicond Sci Technol 25, 055013 (2010).
30
CH Roth, LL Kinney Fundamentals of Logic Design (CL-Engineering, Stamford, CT), pp. 317–345 (2009).
31
N Burgess, Fast ripple-carry adders in standard-cell CMOS VLSI. 20th IEEE Symposium on Computer Arithmetic, eds E Antelo, D Hough, P Lenne (IEEE, Tübingen, Germany), pp. 103–111 (2011).
